６.高周波の積

　もうひとつの方法が高周波の和ではなく積を作ることです。積も和と同様に、各時刻でふたつの波の値を掛け算します。これを電子回路で実現する回路としてはリング・モジュレーターなどが知られています。リング・モジュレーターはそれだけで電気楽器用のエフェクターとして使われますから、名前に聞き覚えがあるかもしれません。

　図2のふたつの波を掛け算したものが図12です。速い振動がさらにゆっくりと振動しているように見えます。和との大きな違いは、このゆっくりした振動が振幅ではなく、波そのものとして現れていることです。三角関数の公式を使うと

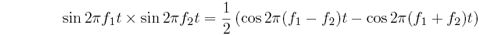
となります。つまり、和のときとは逆に、近い周波数を持つふたつの正弦波の積は、ƒ₁?ƒ₂の正弦波とƒ₁＋ƒ₂の正弦波を足したものと同じなのです（図13）。ƒ₁＋ƒ₂のほうは高周波ですから、ローパスフィルターに通して高周波を捨ててしまえば、残るのは差の振動数を持つ正弦波となります。原理は非常に簡単ですね。簡単なわりにあまり使われていないのは、リング・モジュレーターを組むよりも非線形回路や検波のほうが簡単だからなのでしょうか。実は、最初に見た「和の二乗」でも、式を展開すれば正弦波の積が作られ、そこから周波数ƒ₁? ƒ₂の正弦波が現れます。その意味では積を作ろうが和の二乗を作ろうが基本的な原理は同じです。