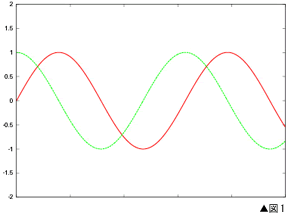|
 正弦波というのはもっとも基本的な波です。たとえば、振り子を小さく揺らしたとき、真下からの振れ角が時間t とともにどう変わるかを描くと図1のようになります（横軸が時刻で縦軸が振れ角）。これが正弦波です。ふたつの波が描かれていますが、これはまったく同じ波を横に（時間方向に）ずらしただけのものです。ギターなどの弦の振動も振れが小さければ正弦波ですし、水面の波を横から見た形も振幅が小さければ正弦波です。どんなものでも、小さく揺らせばその振動は正弦波になると思っておいてください。
図を見てわかるように、正弦波はまったく同じ上下振動を何度も繰り返します。この一回の振動にかかる時間が周期です。一秒間に何回振動するか（つまり1/周期）は周波数とよばれ、Hz（ヘルツ）という単位で表します。この正弦波を表す関数がよく知られた三角関数、つまりsinやcosです。実は図1の波はそれぞれ sin2π/ƒt とcos2π/ƒtを描いたものでした。ƒが周波数です。sinとcosは同じ波を横にずらしただけというわけです。
ところで、正弦波を音にしたものは、たったひとつの周波数を持つ音という意味で純音とよばれます。楽器でいえばフルートの音色あたりが純音に近いでしょうか。バイオリンなどとはずいぶん違う音色です。西洋音楽では多くの場合、440Hzをラの音とします。しかし、楽器のラの音は一般に440Hzの正弦波だけでできているのではなく、もっと高いさまざまな周波数の正弦波を加えたものとなっています。440Hzの音にその2倍、3倍、4倍といった周波数を持つ倍音を加えても、どういうわけか我々の耳にはラとして聴こえるのです。そして、どのような周波数の倍音がどれだけ含まれるかが音色を決めています。同じラの音でもフルートとバイオリンで音色が違うのは、倍音の組み合わせが違うからです。
楽器の音に限らず、あらゆる波は正弦波の足し算に分解できることが知られています。これはフーリエ展開と呼ばれます。テルミンの原理を理解する上では、この正弦波への分解が重要なポイントです。
|
