３.高周波の足し算

　周波数の近いふたつの正弦波（図2）を考えましょう。どちらも±1の範囲で振動するものです。ここでは図を見やすくするために周波数の違いを10％としましたが、実際のテルミンでは差はもっと小さく、1％以下が普通です。このふたつを足し合わせると、図3になります。足し合わせるというのは、各時刻でのふたつの波の値を足すという意味です。図3では細かい振動とそれよりずっと長い周期を持つゆっくりした振幅の変化とが見てとれますね。

　元の波をそれぞれ周波数ƒ₁とƒ₂の正弦波として（ƒ₁のほうがƒ₂より速く振動する、つまりƒ₁ > ƒ₂としましょう）、その和を三角関数の公式を使って計算してみると、

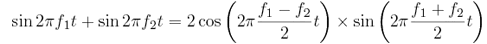
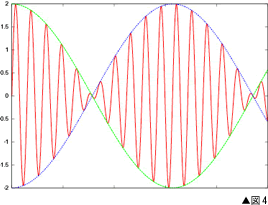となります。つまり、ふたつの正弦波の和は、ふたつの正弦波の積と同じなのです。図3 で見られた細かい振動は、元のふたつの周波数の平均周波数（ƒ₁+ ƒ₂）／2を持ち、一方、全体の振幅はゆっくりと変化します。図4には波の上下の輪郭を描きました。この輪郭の間隔が波の振幅(の二倍) です。上の式を見ると、この振幅変化の周波数は（ƒ₁+ ƒ₂）／2のようですが、振幅には正負が関係ないので、実際はƒ₁?ƒ₂で振動します。

　さて、人間の耳に音として聞こえる可聴域の周波数はだいたい20Hzから20000Hzです。それに対し、テルミンではƒ₁とƒ₂を可聴域上限より10倍から数十倍程度高い高周波に設定します。
もしそれをそのままアンプに通したとしても超音波になるので、耳には聞こえません（実際にはそのような超音波はスピーカーが再生できませんが）。それに対し、振幅変化の周波数ƒ₁? ƒ₂は可聴域に設定されます。たとえば、ƒ₁とƒ₂をそれぞれ300000Hzと297000Hzに設定すれば、その差はƒ₁?ƒ₂ =3000Hzと可聴域の周波数になります。音として取り出したいのは、この振幅の変動です。そのために、速い振動は捨ててしまいましょう。それがローパスフィルターと呼ばれる回路です。この回路では、波を正弦波の和に分解して、指定した周波数以上の周波数を持つ波を捨ててしまいます。

　では、図3の波をローパスフィルターに通すと何が得られるのでしょうか。可聴域以上の振動数を持つ波はすべて捨てられるとしましょう。すると・・・あとには何も残りません。なぜなら、これはもともとƒ₁とƒ₂というふたつの高周波数を足し合わせたものだったからです。それぞれの波がローパスフィルターで捨てられてしまい、何も残らないことになります。