|
図3の輪郭だけを見れば、ƒ1?ƒ2の周波数を持つ波に見えます。可聴域の音を作るなら、この輪郭をそのまま取り出せればよさそうです。そのような方法はあるでしょうか。それがラジオの原理として使われる検波です。まず、波の負の部分を折り返して全部を正にします(図9)。この操作を全波整流といい、回路の中ではダイオードによって実現されます。実はEtherwaveでは負の部分を折り返さずに捨ててしまう半波整流が使われていますが、音を取り出す原理は本質的に同じです。
さて、図9の波は図3を二乗した図5と似てはいるものの、輪郭が正弦波ではありません。実際、この波は少数の正弦波には分解できず、たくさんの(無限の)正弦波の和になります。それを見ていきましょう。まず、図9の波は図10に描いたふたつの波の和に分けることができます。どちらも正弦波ではありませんが、ゆるやかなほうの波の周波数はƒ1?ƒ2なので、仮にこのままアンプに通せば、可聴域の音が聴こえるはずです。
このふたつの波はそれぞれさらに正弦波に分解できます。計算してみると、ゆるやかな波は周波数ƒ1?ƒ2とその2倍、3倍?といった周波数を持つ無限個の正弦波に分解できることがわかります。
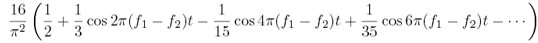
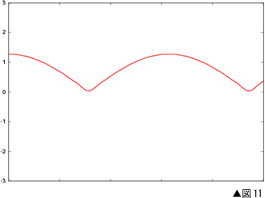 無限個といっても、周波数の高い波ほど小さいのですが。これをローパスフィルターに通して一番周波数の低いƒ1? ƒ2の10倍までの周波数を残すと(たとえば440Hzの10倍は4400Hzですから、まだまだ可聴域です)図11のような波が得られます。この波は倍音をたくさん含むので、正弦波とは違った音色の音になります。 無限個といっても、周波数の高い波ほど小さいのですが。これをローパスフィルターに通して一番周波数の低いƒ1? ƒ2の10倍までの周波数を残すと(たとえば440Hzの10倍は4400Hzですから、まだまだ可聴域です)図11のような波が得られます。この波は倍音をたくさん含むので、正弦波とは違った音色の音になります。
一方、速いほうの波も無限個の正弦波に分解されるのですが、実はその中にはƒ1やƒ2以上の高い周波数を持つ正弦波しか現れません。そこで、図9をローパスフィルターに通すと、この速い波はすべて捨てられてしまいます。
最後に、前と同様にハイパスフィルターで直流成分を捨てればできあがりです。

|