４.非線形回路

　　元の波に比例した波を作りだす回路は線形回路、そうではなく、元の波の二乗や三乗を作り出す回路をまとめて非線形回路と呼びます。もっと複雑な変換でもよく、要するに線形回路以外はすべて非線形回路です。

　本誌では、波を二乗する場合を説明しました。これが非線形回路の基本なので、まずこの例から見ておきましょう。図3の波を二乗したものが図5です。図5には波の輪郭も描いておきました。この輪郭はちょうどƒ₁?ƒ₂の周波数を持つ正弦波になっています。

　さて、三角関数の計算をしてみると

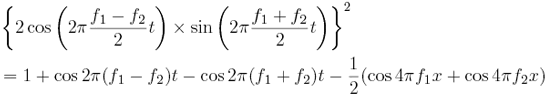
となります。図6に描いた四つの正弦波を全部足すと図5になるということです。四つの正弦波のうち、ひとつだけがƒ₁?ƒ₂の周波数でゆるやかに変化し、他は2ƒ₂ 以上の高周波になっていることに注意してください。したがって、可聴域以上の周波数をローパスフィルターで捨てれば、残るのはƒ₁?ƒ₂の正弦波がひとつだけです。この正弦波はたしかに図5の輪郭と同じ形の波なのですが、振幅は半分です。輪郭の残り半分は、実は高周波の足し合わせでできていたのです。参考までに、図7に三つの高周波の和とƒ₁?ƒ₂の正弦波とを一緒に描いておきます。

　なお、図6のゆっくりした正弦波は正の値の範囲で振動しています（1+cos（ƒ₁?ƒ₂）tなので、1 だけかさ上げされているわけです）。したがって、0を中心として振動する普通の波にするには、かさ上げ分だけ引き下げてやる必要があります。これはハイパスフィルターという回路で実現できます。ハイパスフィルターは名前のとおり、ローパスフィルターと逆に低周波を捨てる働きがあります。最も周波数の低い正弦波は周波数0、つまり一定の値のまま振動しない信号で直流成分と呼ばれます。かさ上げ分の1はまさに直流成分ですから、ハイパスフィルターで捨てられるのです。

　ところで、ここまでは電気信号が電圧なのか電流なのか曖昧なままにしていました。どういう回路を組むかによるのですが、たとえば非線形を生み出す素子としてFET（電界効果トランジスタ）を使うと、入力電圧の二乗に比例する電流が出力されます。入力信号としては図3の電圧変化に直流電圧Vを加えてかさ上げし、正の電圧だけにしたものを使います。それを二乗したものが図8です（V=3としました）。一見、元の波の二乗とは違いますが、二乗を展開すると

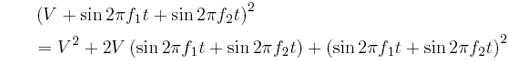
ですから、これはつまり図5の波にƒ₁とƒ₂の正弦波（の2V倍）を足して、さらにV²だけかさ上げしたものなのです。したがって、正弦波の二乗と同じ原理でƒ₁?ƒ₂の正弦波が発生します。