コラム－「時の矢」とアインシュタイン奇跡の1905年

　日常の経験から、私達は時間が過去から未来へと一方向に流れる事を信じて疑わない。この方向性を“時の矢”と呼ぶ。ところが、物理学の基本であるニュートンの古典力学にもマクスウェルの電磁気学にもこんな方向性は存在しない。ニュートンの古典力学は過去に対しても未来に対しても対称的である。つまり、ある現象を撮影してこれを逆まわしにしても、完全にニュートン力学に整合する。しかしながら、逆まわしにすると日常の経験に相反するような一連の現象が存在する。このような現象の多くに、熱の発生が関係している。ストーブの上に氷をおけば、氷はあたたまって溶ける。逆に、ストーブの上においた水がストーブに熱をあたえながら氷として固まる事はあり得ない。こんな不可逆性は、19世紀の産業革命において蒸気機関を設計する経験からよく知られていた。こういった問題を扱う中で生まれた熱力学〔図A〕を、古典力学とどう調和させるかは大問題で、その根底に、生命や情報と深く関連する重要なテーマが潜んでいるのである。

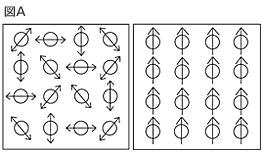
左の図：そもそも熱とは、物体を構成する粒子（分子や原子）が、それぞれの位置の近辺ででたらめに運動している状態が持つ一種の運動エネルギーとされる。 右の図：エネルギーの総量がまったく同じでも、もし粒子の運動の方向と周期がそろうと、物体は“熱”ではなく全体として一方向に運動することになる。 　これはストーブの上に置かれたやかんの水が温まるかわりに、やかんが飛び上がるようなものである。

　1865年、ドイツのクラウジウスは、エネルギーの総量が不変である（熱力学第一法則）という考え方とともに、エネルギーの「質」が時間とともに低下する（熱力学第二法則）という考え方を提案した。つまりエネルギーが劣化する方向こそが「時の矢」だと言うのだ。劣化の程度を示す尺度がエントロピーで、時間とともに全世界のエントロピー総量は増加する。エネルギー保存則と同様、エントロピー増大則は、ある意味では常に成立する「法則」であり、ある意味ではそうあらねばならないという「信念」である。本連載では様々な角度からエントロピーをとりあげるが、今回は、アインシュタイン「奇跡の1905年」との関連からながめてみよう。

　1905年に26才のアインシュタインが書いた5編の論文は、3群に大別される。このうち第4、第5論文は特殊相対性理論に関するもの。1921年、相対性理論に対する風当たりがまだおさまっていなかった事から、アインシュタインのノーベル賞は第1論文の光量子仮説に対して授けられている。そして、第2、第3論文こそが、原子、分子の存在を議論するもの。そもそも相対性理論は古典力学と電磁気学を土台として構築されているから、基本的に「時の矢」を持たない。しかし、第1、第2、第3論文は熱力学第二法則と深く関係していた。

　1906年のボルツマンの自殺に象徴されるように、1905年の時点では、原子、分子の存在はまだ完全に受け入れられた事実ではなかった。化学の教科書は原子や分子といった言葉に満ちていたが、これが本当に“実体”を伴っているのか否かは不明と考えられていたのである。“分子”反対派のリストには、マッハ、ポアンカレ、オストワルドといった有名人が並ぶ。分子の存在を主張するボルツマンの形勢はまだまだ不利で、議論になれば、「エネルギーしか存在しない」と主張するマッハが勝利した。

　ボルツマンが分子の存在を信じたそもそもの理由は、そう考えなければ、時間が一方向に流れる事が説明できなかったからである。コーヒーとミルクをまぜたらミルクコーヒーになるが、放っておいたミルクコーヒーがコーヒーとミルクに分離する事はない。この不可逆性が「時の矢」である。コーヒーもミルクも分子から構成されている事を私達は知っている〔図B〕。カップ全体に2Nの位置があるとする。このそれぞれにコーヒーかミルクの分子（それぞれN個ある）を置いていく。カップの片側にN個のコーヒー（黒）分子がかたまって、反対側にN個のミルク（白）分子がかたまっている状態の種類は、だいたい（N！）×（N！）になる。（N！）は片側のN個の位置にN個のコーヒーもしくはミルク分子だけを置く置き方の種類の数。これに比べて、両者がでたらめにまざった置き方の数（2N！程度）の方が必ず大きいのである。たとえばNがたった10個でも（2N！）と（N！）×（N！）の比は1.8×105：1。Nが大きくなればなるほど両者の比率は大きくなる。だから最初にコーヒーとミルクが分離した状態から出発すると、両者がまじった様々な状態の一つへと簡単に移行するが、再び分離した状態へともどってくる事は“ほとんど”あり得ない。これがボルツマンによる「時の矢」の確率論的な説明の概略である。熱力学がもつ不可逆性と古典力学の可逆性をつなぐために、天文学的な確率を持ち出して、宇宙が始まって以来、一度もおこりえないような確率の現象は実際におこらないと主張するのである。表現を変えるなら、分子の数が天文学的でなければ「時の矢」はときどき逆転することになる。

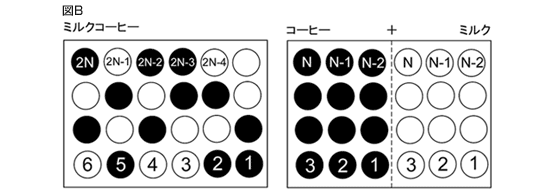ミクロな状態の数の数え方：例えば下の場合、左上のすみに最初に入れるコーヒー分子はN個のうちのどれかなのでN通り、コーヒー分子はこれで一つ減るので、次の位置に入るのはN－１通り……となる。

　ボルツマンの墓には、エントロピー＝定数×logWという有名な式がきざまれている。ここでWはあるマクロな状態（例えばミルクコーヒーとか、コーヒーとミルクが分離したといった）に対応したミクロな状態の数。たしかにボルツマンはこの式と同等の議論を行ったが、この式自身はマックス・プランクが書き下した（次ページ、3月論文）。そのプランクですら、こんな確率論で本当に熱力学第二法則が説明された事になるのかどうか、悩み続けていた。ボルツマンの式が本当に熱力学第二法則を説明しているとしても、ここには時間の「進み方」、つまりどういう物理現象がおきれば、たとえば12分30秒、時間が進むのかを説明する論理はない。

　晩年のアインシュタインは、もはや解決ずみとして相対性理論については語らず、どうしても納得できない量子力学の解釈の問題について議論しようとした。しかし量子力学がまだ生まれる前の当時、若き日のアインシュタインの心をとらえてはなさなかったのは、「分子が存在するはずだ」という確信、そしてその背景にある熱力学の統計性の問題だった。1900年にチューリッヒ工科大学を卒業してから1904年までに5つの論文を書いていたが、いずれも熱力学と分子運動に関する試論だった。部分的には誤りだったり、すでに米国でギブスが発表していた内容だったりしたが、この間、彼は着実に技量をあげていたのである。